New nonlinear least squares solvers in R with {gslnls}
Introduction
Solving a nonlinear least squares problem consists of minimizing a least squares objective function made up of residuals \(g_1(\boldsymbol{\theta}), \ldots, g_n(\boldsymbol{\theta})\) that are nonlinear functions of the parameters of interest \(\boldsymbol{\theta} = (\theta_1,\ldots, \theta_p)'\):
\[ \boldsymbol{\theta}^* \ = \ \arg \min_{\boldsymbol{\theta}} \frac{1}{2} \Vert g(\boldsymbol{\theta}) \Vert^2 \] In the context of regression, this problem is usually formulated as:
\[ \begin{aligned} \boldsymbol{\theta}^* & \ = \ \arg \min_{\boldsymbol{\theta}} \frac{1}{2} \Vert \boldsymbol{y} - f(\boldsymbol{\theta}) \Vert^2 \\ & \ = \ \arg \min_{\boldsymbol{\theta}} \frac{1}{2} \sum_{i = 1}^n (y_i - f_i(\boldsymbol{\theta}))^2 \end{aligned} \]
where \(\boldsymbol{y}\) is the vector of data observations and \(f(\boldsymbol{\theta})\) is a nonlinear model function in terms of the parameters \(\theta_1,\ldots,\theta_p\).
Common solvers used in R
Most standard nonlinear least squares solvers, such as the Gauss-Newton method or the Levenberg-Marquardt algorithm, attempt to find a local minimum of the objective function by making iterative steps in the direction of the solution informed by the gradient of a first- or second-order Taylor approximation of the nonlinear objective function.
The default function to solve nonlinear least squares problems in R, nls(), includes the following gradient-based solvers:
"default", the Gauss-Newton method;"plinear", the Golub-Pereyra algorithm for partially linear least-squares problems;"port", thenls2solalgorithm from the Port library with parameter bounds constraints.
External R-packages aimed at nonlinear least squares optimization include the popular minpack.lm package or John Nash’s nlsr package. The minpack.lm package provides an interface to a modified Levenberg-Marquardt algorithm from the MINPACK library. The nlsr package implements a variant of the Marquardt algorithm (Nash (1977)) with a strong emphasis on symbolic differentiation of the nonlinear model function. A comprehensive overview of R-packages to solve nonlinear least squares problems can be found in the Least-Squares Problems section of the CRAN Optimization task view.
New GSL nonlinear least squares solvers
The new gslnls-package augments the existing suite of nonlinear least squares solvers available in R by providing R bindings to nonlinear least squares optimization with the GNU Scientific Library (GSL)
using the trust region methods implemented by the gsl_multifit_nlinear and gsl_multilarge_nlinear modules. These modules were added in GSL version 2.2 (released in August 2016) and the available C routines have been thoroughly tested and are in widespread use in scientific computing. The mathematical background of the nonlinear least squares algorithms and available control parameters are documented in detail in Galassi et al. (2009).
The following trust region methods to solve nonlinear least-squares problems are available in the gslnls-package:
How/when to use {gslnls}
The function gsl_nls() solves small to moderate sized nonlinear least-squares problems using either numeric or symbolic differentiation of the Jacobian matrix. For (very) large problems, where factoring the full Jacobian matrix becomes prohibitively expensive, the gsl_nls_large() function can be used to minimize the least squares objective. The gsl_nls_large() function is also appropriate for systems with sparse structure in the Jacobian matrix allowing to reduce memory usage and further speed up computations. Both functions use the same interface as R’s default nls() function, similar to minpack.lm::nlsLM(), and the returned fit objects inherit from the class "nls". For this reason, all generic functions available for "nls"-objects, such as summary(), confint(), predict(), etc., are also applicable to objects returned by gsl_nls() or gsl_nls_large().
BoxBOD regression problem
As a demonstrating example, consider the Biochemical Oxygen Demand (BoxBOD) regression problem from (Box et al. 2005, Ch. 10), also listed as one of the test problems in the nonlinear regression section of the NIST StRD archive. Biochemical Oxygen Demand is used as a measure of pollution produced by domestic or industrial wastes. In the BoxBOD data, the Biochemical Oxygen demand was determined by mixing a small portion of chemical waste with pure water and measuring the reduction in dissolved oxygen in the water for six different incubation periods (in separate bottles at a fixed temperature). Physical considerations suggest that the nonlinear relation between the number of incubation days and the BOD response can be described by an exponential model of the form:
\[ f(\boldsymbol{\theta}) = \theta_1 (1 - \exp(-\theta_2 x)) \] with \(\theta_2\) the overall rate constant and \(\theta_1\) the maximum or asymptotic BOD value. According to (Box et al. 2005), the least squares objective is minimized at the parameter values \(\hat{\theta}_1 = 213.81\) and \(\hat{\theta}_2 = 0.5472\), with a residual sum-of-squares value of \(S_R = 1168\). The data and the exponential model evaluated at the least squares parameter estimates are displayed in the plot below.
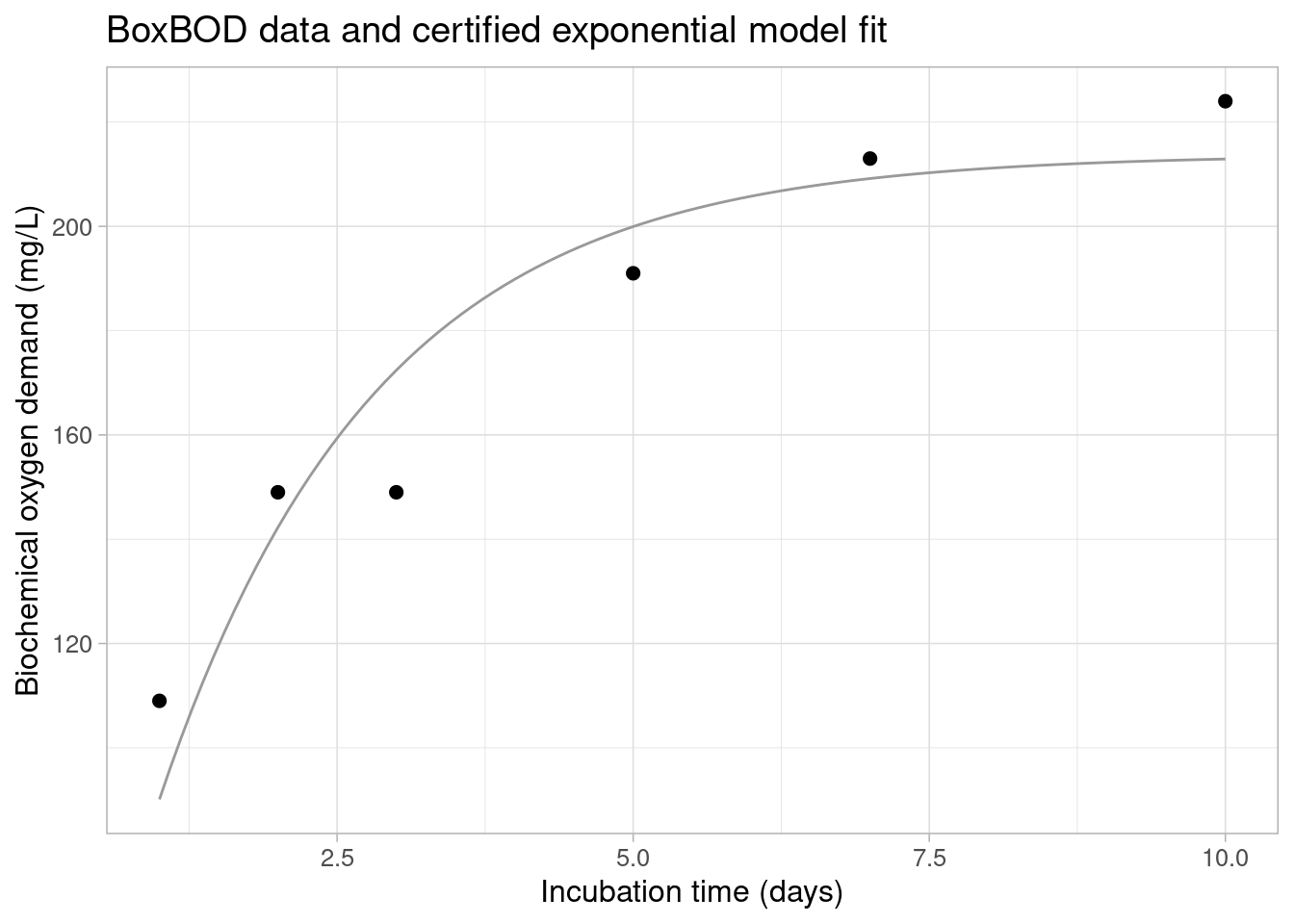
NLS model fits
For the purpose of testing, the NIST StRD archive suggests several increasingly difficult sets of parameter starting values. To solve the regression problem, we choose the set of starting values \(\boldsymbol{\theta}^{(0)} = \{1, 1\}\) furthest away from the least squares solution. Solving this nonlinear regression problem is particularly difficult due to the fact that the parameters live on different scales, as well as the fact that the problem is susceptible to parameter evaporation (i.e. parameters diverging to infinity). This also becomes apparent when trying to solve the least squares problem using the nls Port algorithm and the minpack.lm version of the Levenberg-Marquardt algorithm:
## data
BoxBOD <- data.frame(
y = c(109, 149, 149, 191, 213, 224),
x = c(1, 2, 3, 5, 7, 10)
)## base R (port algorithm)
nls(
formula = y ~ theta1 * (1 - exp(-theta2 * x)),
data = BoxBOD,
start = list(theta1 = 1, theta2 = 1),
trace = TRUE,
algorithm = "port"
)
#> 0: 93191.191: 1.00000 1.00000
#> 1: 91256.158: 2.84913 2.55771
#> 2: 18920.595: 104.102 10.1516
#> Error in numericDeriv(form[[3L]], names(ind), env, dir = -1 + 2 * (internalPars < : Missing value or an infinity produced when evaluating the model## minpack.lm (Levenberg-Marquardt algorithm)
minpack.lm::nlsLM(
formula = y ~ theta1 * (1 - exp(-theta2 * x)),
data = BoxBOD,
start = list(theta1 = 1, theta2 = 1),
trace = TRUE
)
#> It. 0, RSS = 186382, Par. = 1 1
#> It. 1, RSS = 40570.3, Par. = 100.854 110.949
#> It. 2, RSS = 9771.5, Par. = 172.5 110.949
#> It. 3, RSS = 9771.5, Par. = 172.5 110.949
#> Error in nlsModel(formula, mf, start, wts): singular gradient matrix at initial parameter estimatesSolving the regression problem with gsl_nls() using the GSL version of the Levenberg-Marquardt algorithm (with default numeric differentiation of the Jacobian), we set the damping strategy in the trust region subproblem to scale = "levenberg". This generally tends to work better than the default (scale-invariant) strategy scale = "more" for problems susceptible to parameter evaporation1:
library(gslnls) ## v1.1.1
## GSL (Levenberg-Marquardt algorithm)
(fit <- gsl_nls(
fn = y ~ theta1 * (1 - exp(-theta2 * x)),
data = BoxBOD,
start = list(theta1 = 1, theta2 = 1),
algorithm = "lm",
control = list(scale = "levenberg")
))
#> Nonlinear regression model
#> model: y ~ theta1 * (1 - exp(-theta2 * x))
#> data: BoxBOD
#> theta1 theta2
#> 213.8094 0.5472
#> residual sum-of-squares: 1168
#>
#> Algorithm: multifit/levenberg-marquardt, (scaling: levenberg, solver: qr)
#>
#> Number of iterations to convergence: 18
#> Achieved convergence tolerance: 1.362e-09Another way to achieve convergence to the correct parameter values is to switch the solver to the Levenberg-Marquardt algorithm with geodesic acceleration correction. This extended algorithm has been shown to provide more stable convergence compared to the standard Levenberg-Marquardt algorithm for a large class of test problems due to the extra acceleration correction (Transtrum and Sethna 2012).
## GSL (Levenberg-Marquardt w/ geodesic acceleration)
gsl_nls(
fn = y ~ theta1 * (1 - exp(-theta2 * x)),
data = BoxBOD,
start = list(theta1 = 1, theta2 = 1),
algorithm = "lmaccel"
)
#> Nonlinear regression model
#> model: y ~ theta1 * (1 - exp(-theta2 * x))
#> data: BoxBOD
#> theta1 theta2
#> 213.8094 0.5472
#> residual sum-of-squares: 1168
#>
#> Algorithm: multifit/levenberg-marquardt+accel, (scaling: more, solver: qr)
#>
#> Number of iterations to convergence: 26
#> Achieved convergence tolerance: 2.457e-09The output printed by gsl_nls() is analogous to that of nls() (or minpack.lm::nlsLM()) and all the usual methods for objects of class "nls" can be applied to the fitted model object:
## model summary
summary(fit)
#>
#> Formula: y ~ theta1 * (1 - exp(-theta2 * x))
#>
#> Parameters:
#> Estimate Std. Error t value Pr(>|t|)
#> theta1 213.8094 12.3545 17.306 6.54e-05 ***
#> theta2 0.5472 0.1046 5.234 0.00637 **
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 17.09 on 4 degrees of freedom
#>
#> Number of iterations to convergence: 18
#> Achieved convergence tolerance: 1.362e-09
## asymptotic confidence intervals
confint(fit, method = "asymptotic", level = 0.95)
#> 2.5 % 97.5 %
#> 1 179.5077734 248.1110349
#> 2 0.2569326 0.8375425The predict method extends the existing predict.nls method by allowing for calculation of asymptotic confidence and prediction (tolerance) intervals in addition to prediction of the expected response:
## asymptotic prediction intervals
predict(fit, interval = "prediction", level = 0.95)
#> fit lwr upr
#> [1,] 90.11087 35.41443 144.8073
#> [2,] 142.24413 86.43974 198.0485
#> [3,] 172.40562 118.92302 225.8882
#> [4,] 199.95092 147.58019 252.3217
#> [5,] 209.17076 154.36050 263.9810
#> [6,] 212.91114 155.51375 270.3085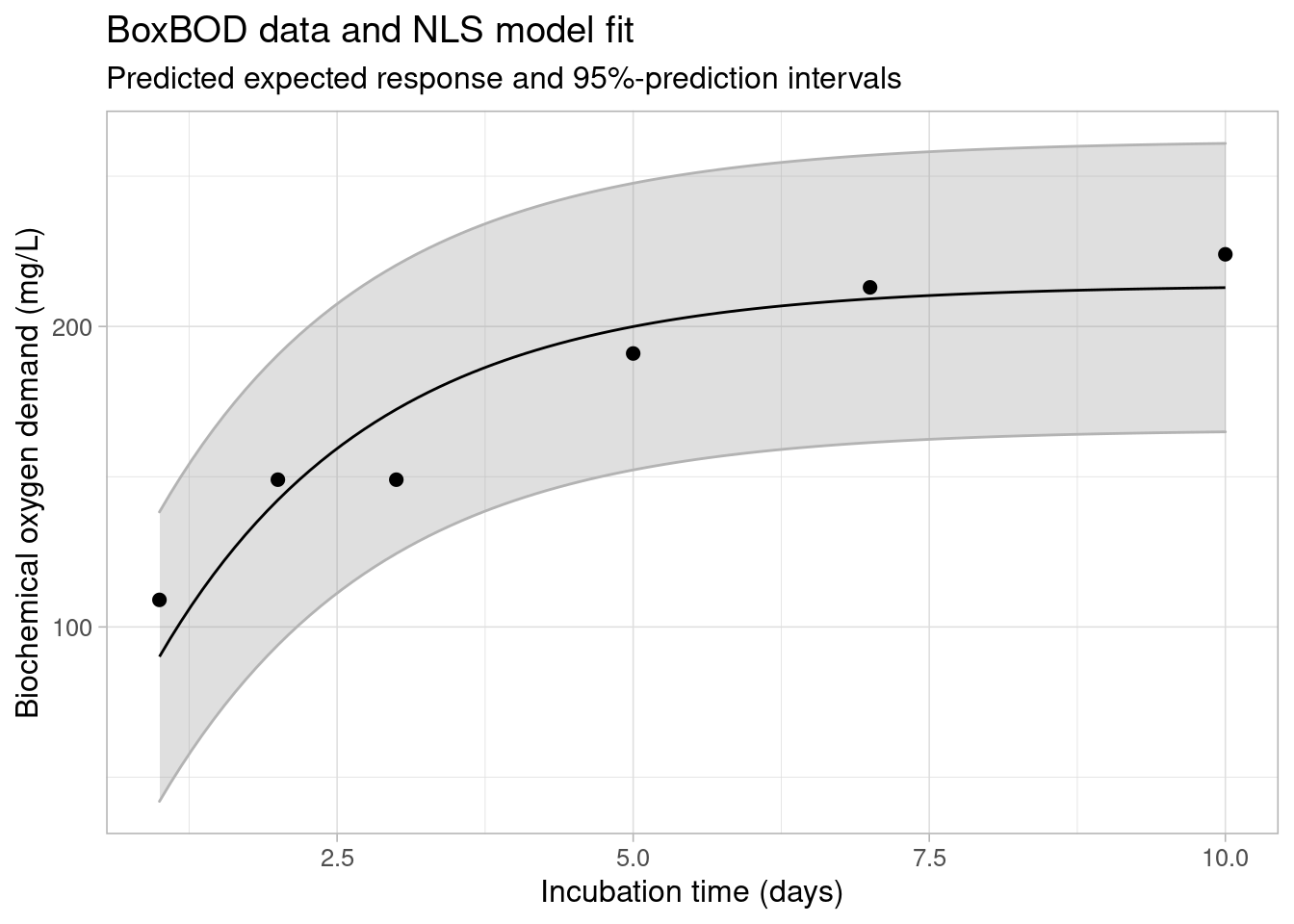
Parameter constraints
The GSL nonlinear least squares routines do not allow bounds constraints to be imposed on the parameters. This is in contrast to other routines available in R, such as those provided by minpack.lm. For the purpose of pure optimization, imposing lower and upper bounds constraints on the parameters is common practice, but statisticians have generally been wary of imposing hard parameter constraints due to complications in evaluating interval estimates for the parameters or functions thereof (Nash (2022)). In particular, imposing parameter constraints in solving the BoxBOD test problem with the minpack.lm version of the Levenberg-Marquardt algorithm, the model parameters simply run away to the boundaries, which does not improve convergence in any way:
## Levenberg-Marquardt with parameter constraints
minpack.lm::nlsLM(
formula = y ~ theta1 * (1 - exp(-theta2 * x)),
data = BoxBOD,
start = list(theta1 = 1, theta2 = 1),
lower = c(theta1 = 0, theta2 = 0),
upper = c(theta1 = 500, theta2 = 5)
)
#> Nonlinear regression model
#> model: y ~ theta1 * (1 - exp(-theta2 * x))
#> data: BoxBOD
#> theta1 theta2
#> 172.8 5.0
#> residual sum-of-squares: 9624
#>
#> Number of iterations to convergence: 3
#> Achieved convergence tolerance: 1.49e-08If there are known physical constraints for the parameters or if the model function cannot be evaluated in certain regions of the parameter space, it often makes sense to reparameterize the model, such that the model parameters are unconstrained. If prior information is available on the target parameter values, update the starting values or include some type of parameter penalization (i.e. a weighting function). This is preferable to imposing hard parameter constraints which essentially assign uniform weights inside the parameter bounds and infinite weights elsewhere2.
Model reparameterization
Below, we reparameterize the BoxBOD regression model by substituting \(\theta_1 = \exp(\eta_1)\) and \(\theta_2 = \exp(\eta_2)\) in the exponential model, such that \(\eta_1, \eta_2\) are unconstrained and \(\theta_1, \theta_2\) are positive. The model is refitted with the gslnls version of the Levenberg-Marquardt algorithm using the transformed starting values \(\boldsymbol{\eta}^{(0)} = \{0, 0\}\):
## GSL (Levenberg-Marquardt algorithm)
(refit <- gsl_nls(
fn = y ~ exp(eta1) * (1 - exp(-exp(eta2) * x)),
data = BoxBOD,
start = list(eta1 = 0, eta2 = 0),
control = list(scale = "levenberg")
))
#> Nonlinear regression model
#> model: y ~ exp(eta1) * (1 - exp(-exp(eta2) * x))
#> data: BoxBOD
#> eta1 eta2
#> 5.3651 -0.6029
#> residual sum-of-squares: 1168
#>
#> Algorithm: multifit/levenberg-marquardt, (scaling: levenberg, solver: qr)
#>
#> Number of iterations to convergence: 11
#> Achieved convergence tolerance: 2.959e-08Remark: The new confintd method, based on an application of the delta method, can be used to evaluate asymptotic confidence intervals for the parameters in the original model:
## delta method confidence intervals
confintd(refit, expr = c("exp(eta1)", "exp(eta2)"), level = 0.95)
#> fit lwr upr
#> exp(eta1) 213.8093867 179.5077650 248.1110085
#> exp(eta2) 0.5472377 0.2569327 0.8375428Large NLS problems
As an example of a large nonlinear least squares problem, we reproduce the Penalty function I test problem from (Moré, Garbow, and Hillstrom 1981, pg. 26) among others3. For a given number of parameters \(p\), the \(n = p + 1\) residuals forming the least squares objective are defined as:
\[ \left\{ \begin{aligned} g_i & \ = \sqrt{\alpha}(\theta_i + 1), \quad i = 1,\ldots,p \\ g_{p + 1} & \ = \Vert \boldsymbol{\theta} \Vert^2 - \frac{1}{4} \end{aligned} \right. \]
with fixed constant \(\alpha = 10^{-5}\) and unknown parameters \(\boldsymbol{\theta} = (\theta_1,\ldots, \theta_p)'\). Note that the residual \(g_{p + 1}\) adds an \(L_2\)-regularization constraint on the parameter vector thereby making the system nonlinear.
For large problems, it is generally discouraged to rely on numeric differentiation to evaluate the Jacobian matrix. Instead it is often better to obtain the Jacobian either analytically, or through symbolic or automatic differentiation. In this example, the \((p + 1) \times p\)-dimensional Jacobian matrix is straightforward to derive analytically:
\[ \boldsymbol{J}(\boldsymbol{\theta}) \ = \ \left[ \begin{matrix} \frac{\partial g_1}{\partial \theta_1} & \ldots & \frac{\partial g_1}{\partial \theta_p} \\ \vdots & \ddots & \vdots \\ \frac{\partial g_{p+1}}{\partial \theta_1} & \ldots & \frac{\partial g_{p+1}}{\partial \theta_p} \end{matrix} \right] \ = \left[ \begin{matrix} \sqrt{\alpha} \boldsymbol{I}_{p \times p} \\ 2 \boldsymbol{\theta}' \end{matrix} \right] \]
where \(\boldsymbol{I}_{p \times p}\) denotes the \((p \times p)\) identity matrix.
The model residuals and Jacobian matrix can be written as a function of the parameter vector \(\boldsymbol{\theta}\) as follows:
## model definition
g <- function(theta) {
structure(
c(sqrt(1e-5) * (theta - 1), sum(theta^2) - 0.25), ## residuals
gradient = rbind(diag(sqrt(1e-5), nrow = length(theta)), 2 * t(theta)) ## Jacobian
)
}Here, the Jacobian is returned in the "gradient" attribute of the evaluated residual vector (as in a selfStart model) from which it is detected automatically by gsl_nls() or gsl_nls_large(). Instead, a function returning the evaluated Jacobian can also be passed explicitly to the jac argument.
First, we minimize the least squares objective with a call to gsl_nls() by passing the nonlinear model as a function (instead of a formula) and setting the response vector y to a vector of zeros4. The number of parameters is set to \(p = 500\) and the starting values \(\theta^{(0)}_i = i\) are taken from (Moré, Garbow, and Hillstrom 1981).
## number of parameters
p <- 500
## standard Levenberg-Marquardt
system.time({
small_lm <- gsl_nls(
fn = g,
y = rep(0, p + 1),
start = 1:p,
control = list(maxiter = 500)
)
})
#> user system elapsed
#> 29.289 0.043 29.371
cat("Residual sum-of-squares:", deviance(small_lm), "\n")
#> Residual sum-of-squares: 0.00477904Second, we fit the same model, but with a call to gsl_nls_large() using the iterative Steihaug-Toint Conjugate Gradient algorithm. This algorithm avoids the need for computationally expensive factorization of the normal equations matrix \(\boldsymbol{J}(\boldsymbol{\theta})'\boldsymbol{J}(\boldsymbol{\theta})\), thereby drastically reducing the runtime for this example:
## large-scale Steihaug-Toint
system.time({
large_cgst <- gsl_nls_large(
fn = g,
y = rep(0, p + 1),
start = 1:p,
algorithm = "cgst",
control = list(maxiter = 500)
)
})
#> user system elapsed
#> 0.957 0.000 0.958
cat("Residual sum-of-squares:", deviance(large_cgst), "\n")
#> Residual sum-of-squares: 0.004778862Sparse Jacobian matrix
The Jacobian matrix \(\boldsymbol{J}(\boldsymbol{\theta})\) in the current problem is very sparse in the sense that it contains only a small number of nonzero entries. The gsl_nls_large() function also accepts the evaluated Jacobian as a sparse matrix of Matrix-class "dgCMatrix", "dgRMatrix" or "dgTMatrix". To illustrate, we can update the model function to return the sparse Jacobian as a "dgCMatrix" instead of a dense numeric matrix:
## sparse model definition
gsp <- function(theta) {
structure(
c(sqrt(1e-5) * (theta - 1), sum(theta^2) - 0.25),
gradient = rbind(Matrix::Diagonal(x = sqrt(1e-5), n = length(theta)), 2 * t(theta))
)
}Comparing the performance of the Levenberg-Marquardt and Steihaug-Toint algorithms with respect to the initial dense Jacobian definition, besides a slight improvement in runtimes, the required amount of memory is significantly smaller for the model functions returning a sparse Jacobian matrix than the model functions returning a dense Jacobian matrix:
## computation times and allocated memory
bench::mark(
"Dense LM" = gsl_nls_large(fn = g, y = rep(0, p + 1), start = 1:p, algorithm = "lm", control = list(maxiter = 500)),
"Dense CGST" = gsl_nls_large(fn = g, y = rep(0, p + 1), start = 1:p, algorithm = "cgst"),
"Sparse LM" = gsl_nls_large(fn = gsp, y = rep(0, p + 1), start = 1:p, algorithm = "lm", control = list(maxiter = 500)),
"Sparse CGST" = gsl_nls_large(fn = gsp, y = rep(0, p + 1), start = 1:p, algorithm = "cgst"),
check = FALSE,
min_iterations = 5
)
#> Warning: Some expressions had a GC in every iteration; so filtering is disabled.
#> # A tibble: 4 × 6
#> expression min median `itr/sec` mem_alloc `gc/sec`
#> <bch:expr> <bch:tm> <bch:tm> <dbl> <bch:byt> <dbl>
#> 1 Dense LM 4.05s 4.15s 0.243 1.32GB 7.19
#> 2 Dense CGST 890.15ms 919.91ms 1.06 864.49MB 19.9
#> 3 Sparse LM 3.74s 3.76s 0.262 29.46MB 0.524
#> 4 Sparse CGST 346.51ms 347.07ms 2.88 21.22MB 3.45References
https://www.gnu.org/software/gsl/doc/html/nls.html#c.gsl_multilarge_nlinear_scale.gsl_multilarge_nlinear_scale_levenberg.↩︎
In a Bayesian context, the use of uniform priors is generally discouraged as well.↩︎
The same problem is also used as an example in the GSL documentation.↩︎
Alternatively
minpack.lm::nls.lm()also accepts afunction(instead of aformula) returning the vector of residuals, but in this example reaches the maximum allowed number of iterations (maxiter = 1024) without convergence.↩︎